Colony – A brief history of timing

In another guest post, Matt Bentley provides us with new insights into container performance, analyzing the implications on iteration costs of his implementation of the “bucket array” concept.

Back in 2014 I began designing a game engine. Experienced programmers and curmudgeonly lecturers will tell you that if you make a game engine, you’ll never make a game – which is true, but sort of irrelevant. You will learn so much from making a game engine, you probably won’t care about the game by the end of it. The main reason I wanted to develop a game engine was that I was tired of seeing very basic 2D games with incredibly bad performance even on fast computers. If we got 15 frames-per-second on Intel 386 processors in the 1990s, why was it so hard for modern 2D games to achieve the same speed on exponentially-better hardware?

 

The main reason seemed to be inefficient game engines and the use of non-native graphics protocols with poor backwards compatibility for older equipment. Most games seemed to be either running under Unity, which at the time was very slow for 2D work, or they required OpenGL 2.0, which at the time was not supported on a lot of lower-specification equipment such as my 2009 Intel Atom-based netbook (still running to this day, BTW). So the first thing I did was develop my engine on top of the SDL2 (Simple Directmedia Layer) framework, which uses the native graphics protocol of whatever platform it’s running on: DirectX for Windows, Quartz for MacOS, etcetera.

 

The second thing was to try and cater to a wide range of 2D gaming scenarios, while introducing as little overhead as possible. This meant learning about quadtrees, the various containers available in the C++ standard library, and a bunch of other performance-related stuff. Contrary to what many non-game-developers think, designing a game engine is one of the most complicated things you can do, programming-wise. It really is quite mind-blowing. The number of interactions between different parts of a game is phenomenal. Despite that, I eventually managed to come up with something reasonably comprehensible.

 

However, I kept on running up against a particular scenario. To explain further, you need to understand that most data in games has the following characteristics:

1. It gets introduced at some point during a level.

2. It gets removed or destroyed at some point during a level.

3. It has a vast number of interactions and dependencies on other pieces of data (textures, sounds, etcetera).

4. There is almost always more than one of a given type of data.

5. The sequential order of the data is generally not relevant.

 

This is not a good fit for C++’s std::vector data container, which, if you were to believe most C++ folk, is the container you should use for most things. The reason why it isn’t a good fit is because vectors reallocate their contained objects (elements) in memory, both when inserting, and when erasing any element which isn’t at the back of the vector. This means pointers to vector elements get invalidated, and then all your element interactions and dependencies no longer work. Sure, you can access elements via indexes instead of pointers, but your indexes will also get invalidated if you erase from, or insert to, anywhere but the back of the vector.

 

There’s a wide range of workarounds for std::vector in this situation, each of which I could write a post on, but none are widely suited to all game engine scenarios, and all create computational overhead. There are other containers in the C++ standard library which do ensure pointer validity post-insertion/erasure, like include std::map and std::list, but all of these have terrible iteration performance on modern hardware. This is because they do not allocate their elements linearly in memory i.e. in one memory chunk, but instead allocate elements individually.

 

By comparison a std::vector is basically just an array which gets copied to another, larger array when it’s full and an insertion occurs, so it is 100% linear in memory. Due to the fact that modern CPUs read data into the cache from main memory in contiguous chunks, if you read one element from a std::vector you end up reading a bunch of subsequent elements into cache at the same time, provided the elements in question are at least half the read chunk’s size. If you’re processing elements sequentially, this means that by the time you process the second element, it’s already in the cache.

 

If you’re interested in this subject I’m sure you’ve seen this table or something very much like it before, but for those who haven’t I’ll reproduce it here:

execute typical instruction	1/1,000,000,000 sec = 1 nanosec
fetch from L1 cache memory	0.5 nanosec
branch misprediction	5 nanosec
fetch from L2 cache memory	7 nanosec
Mutex lock/unlock	25 nanosec
fetch from main memory	100 nanosec
send 2K bytes over 1Gbps network	20,000 nanosec
read 1MB sequentially from memory	250,000 nanosec
fetch from new disk location (seek)	8,000,000 nanosec
read 1MB sequentially from disk	20,000,000 nanosec
send packet US to Europe and back	150 milliseconds = 150,000,000 nanosec

---

(source: http://norvig.com/21-days.html#answers)

For most modern computers, accessing data in the L1 cache is between 100-200 times faster than accessing it in main memory. That’s a big difference. So when you have a lot of data to process, from the performance side of things you want it to be linearly allocated in memory and you want to process it sequentially. When you use a std::list, you may have the benefit of being able to preserving pointer validity to individual elements regardless of insertion/erasure, but because it has no guarantee of linear memory storage, subsequent elements are unlikely to be read into the cache at the same time as the first element, so speed of sequential processing becomes poor.

 

Once I understood this, I started looking into alternatives. The first solution I came up with was in retrospect, fairly silly and over-complicated. It was essentially a map-like container using the original pointers to the elements as keys. The architecture of this was two vectors: one of pointer + index pairs, one of the elements themselves. When you accessed an element via its pointer, the container did a lookup across the pointer pairs and returned the element via its index into the second vector. When reallocation of elements occurred in the second vector due to erasures or insertions, the indexes in the first vector would get updated.

 

I sent this off to Jonathan Blow, designer of the games Braid and The Witness, who in those days was somewhat less famous and seemingly had more time to spend educating such a neophyte. His take was: not very good. I asked him what ‘good’ might look like in this scenario, and he talked about having an array of pointers, each pointing to elements in a second array, then updating the first array when elements in the second reallocated. Then the programmer would store pointers to the pointers in the first array, and double-dereference to obtain the elements themselves. But he also mentioned another approach, of having a linked list of multiple memory chunks.

 

The advantage of the second approach was that no reallocation would have to occur upon expansion of the container capacity. That interested me more, so I started work on something similar, using a boolean skipfield to indicate erased elements so that they could be skipped during iteration and no reallocation of elements would be necessary during erasure either. I would later find out that this general concept is often known as a ‘bucket array’ in games programming, also existing in other programming domains under various names. But that would not be for several years, so for now I called it a ‘colony’, like a human colony where people come and go all the time, houses are built and destroyed, etcetera.

 

My implementation actually ended up being substantially different from most bucket arrays; typically, all of the ‘buckets’ or memory blocks are of a fixed size. Colony followed a common-sense principle espoused by most implementations of std::vector, which is: every time the container has to expand, it doubles its capacity. This works well when the programmer doesn’t know in advance how many elements will be stored, as the container can start with a very small allocation of memory for first insertion, and then grow appropriately based on how many insertions have occurred. I also made minimum/maximum block sizes specifiable, to better fit particular scenarios and cache sizes.

 

In addition, bucket arrays do not tend to reuse the memory of erased elements; instead, new elements are inserted at the back of the container, and memory blocks are freed to the OS when they become empty of elements. Colony keeps a record of erased element memory locations and reuses those locations when inserting new elements. This is possible because it is an unordered (but sortable) container. Doing so has two performance advantages: fewer allocations/deallocations occur because memory is reused, and reusing memory spaces helps keep elements more linear in memory, rather than preserving large chunks of unused memory between non-erased elements.

 

By 2015 I’d managed to make colony into a fully-fledged (if buggy) C++ template container, meaning that it could be used to store any data type. Performance was pretty good, according to my (also buggy at that time) benchmarks. There was still one thing that was bugging me though. Bit-level access is slower than byte-level access on a modern computer, but using a full byte for a boolean value in a skipfield seemed wasteful – specifically, it uses 8 times the amount of memory it needs. So I thought about how I might leverage the extra bits to create better performance. I had a few ideas, but I downplayed them in my own mind.

 

One day at GDC 2015 New Zealand, after I’d presented a talk on colony, I got to talking with an ex-Lionhead developer who had moved back to NZ. The guy was so arrogant it made me a little bit angry. That night, lying in bed and fuming slightly, I channeled the anger into thinking about that particular problem with colony, and suddenly, going over the equations in my head, I had a solution. Pro-tip: never make a programmer angry, you might make them better at programming. The next day as I bussed back home I started coding what would eventually be called the high-complexity jump-counting skipfield pattern.

 

The idea is extremely simple: instead of letting all those extra bits in the byte go to waste, use them to count the number of erased elements you have to skip to reach the next unskipped element. So whereas a boolean skipfield looks like this (where ‘0’ indicates an element to process and ‘1’ indicates one which is erased/skipped):

1 0 0 0 0 1 1 1 1 0 0 1 1

The equivalent high-complexity jump-counting skipfield looks like this:

1 0 0 0 0 4 2 3 4 0 0 2 2

 

The first ‘4’, of course, indicates that we are to skip four erased element memory spaces at that point. The second 4 is the same but for reverse iteration. The numbers in between – well it gets a little complicated, but basically they get used when erased element memory spaces get reused, so that the run of erased elements (or “skipblock”) can be broken apart when a non-back/front memory space gets re-used. Now, of course if we’re expressing the skipfield in bytes, that means we can only count up to 255 skipped elements at a time. This effectively limits the capacity of each memory block in the colony to 256 elements, which is not great for cache friendliness, unless the type itself is reasonably large.

 

So I upgraded the byte-sized skipfield token to an unsigned short (equivalent to uint_least16). This upgraded the maximum possible capacity of individual memory blocks to 65535 elements on most platforms. I did try unsigned ints, for a maximum possible capacity of 4294967295, but this failed to give any improvement in terms of performance across all types. Eventually the skipfield type became a template parameter, so that users could downgrade to the unsigned char type, and save memory, and performance for numbers of elements under 1000.

 

To get back to iteration, while the iteration code for a boolean skipfield looks like this in C++ (where ‘S‘ is the skipfield array and ‘i‘ is the current index into both the skipfield array and its corresponding array of elements):

do {
  ++i;
} while (S[i] == 1);

The iteration code for the jump-counting skipfield looks like this:

++i;
i += S[i];

 

Which means compared to a boolean skipfield a jump-counting skipfield iteration (a) has no looping, and therefore fewer instructions per iteration, and (b) has no branching. (a) is important for large amounts of data. Imagine if you had 6000 erased elements in a row being skipped on a boolean skipfield – that would mean 6000 reads of the skipfield and 6000 branch instructions, just to find the next non-erased element! By comparison the jump-counting skipfield only needs one skipfield read per iteration and 2 calculations total. (b) is important because on modern processors, branching has a problematic performance impact due to CPU pipelining.

 

Pipelines allow multiple sequential instructions to execute in parallel on a CPU when appropriate; this only happens if the instructions do not depend on each other’s results for input. Branching throws off the efficiency of pipelining by preventing all subsequent sequential instructions from being processed until this one decision has occurred. Branch prediction algorithms in CPUs attempt to alleviate this problem by predicting, based on past branch decisions, what the branch decision is likely to be and pre-storing the code resulting from that decision in the pipeline.

 

But some CPUs are better than others at this, and regardless, there is always some performance impact from a failed branch prediction. Take the following benchmarks comparing an early version of colony using a boolean skipfield to denote erasures, versus std::vector using a boolean skipfield to denote erasures, and a colony using a jump-counting skipfield. The tests were performed on a Core2 processor – now an outdated CPU – but demonstrate a point. They show time taken to iterate, after a certain percentage of all elements have been erased, at random:

These benchmarks show an odd but ultimately predictable pattern. When no elements have been erased, the std::vector is fastest while the boolean version of colony is slowest. When 25% of all elements have been erased, suddenly the jump-counting colony is significantly faster than both boolean approaches. When 50% have been erased, there is a massive drop in performance for the boolean approaches, but the jump-counting skipfield performs better again. When 75% erasures is reached, the two boolean approaches perform better than they did at 50% erasures, as does the jump-counting approach. Why is this?

 

Well, it turns out there is a significant cost to a failed branch prediction on an Intel Core2 processor – later models of Intel processors have better performance here but are still affected. When no erasures have occurred, the branch predictor can be correct every time, which is why the vector with the boolean skipfield is faster at that point (due to its singular memory block as opposed to colony’s multiple memory blocks). However once you get 25% erasures the branch prediction can only be correct 75% of the time, statistically speaking. When it fails the CPU has to flush its pipeline contents.

 

At 50% random erasures the branch prediction basically cannot function – half or more of all branch predictions will fail. Once we get to 75% erasures, the branch prediction is once again correct 75% of the time, and so the boolean skipfield performance increases compared to 50%. Meanwhile, the only relevant performance factor for the jump-counting skipfield, which has no branch instructions during iteration, is the number of total reads of the skipfield it must perform, which reduces proportionately to the percentage of erasures. From this example, we can already see that a jump-counting skipfield is more scalable than a boolean skipfield.

 

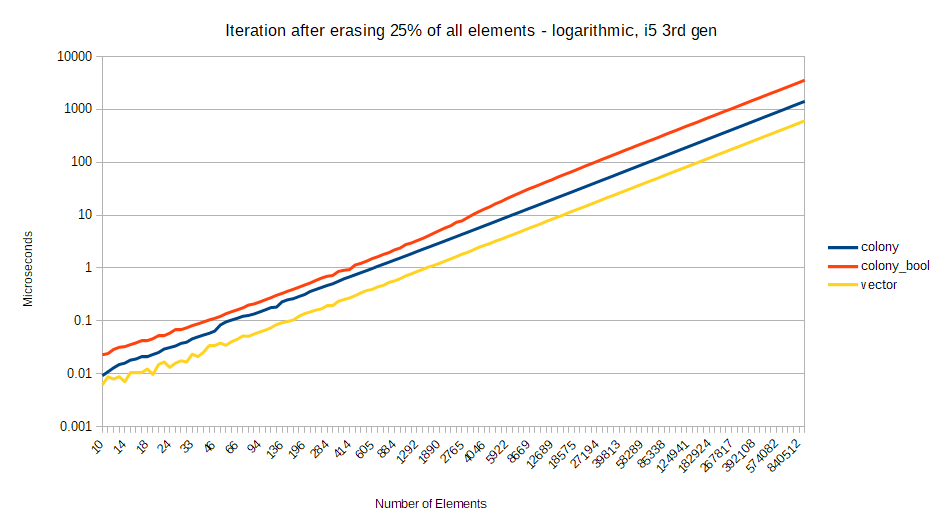
Meanwhile for CPU’s without such severe penalties for branch prediction failure, the difference in results between boolean and jump-counting skipfields tends to scale proportionately to the erasure percentage. For a Intel i5 3rd generation processor, the results are as follows. This time I’m displaying logarithmic scale to give a clearer view of differences for small numbers of elements. Also I’m using a straight vector instead of a vector with bools for erasures, just to give some idea of how colony element traversal performs compared to linear memory traversal without gaps:

 

As you can see, the colony with a jump-counting skipfield remains relatively equidistant from std::vector at all levels of erasure, with performance increasing as the number of erasures increases. Colony with a boolean skipfield gets proportionally worse as the percentage of erasures increases; on average 2x longer duration than jump-counting at 25% erasures, 3x longer at 50% erasures, and 4x longer at 75% erasures. This reflects the ever-increasing number of instructions necessary to reach the next element when using a boolean skipfield. Even so, there is still slightly worse performance at 50% erasures for the boolean skipfield than at 75% erasures – indicating once again that branch prediction failure plays a role in results. The jump-counting skipfield’s branch-free O(1) iteration instruction size means it suffers neither of these fates.

 

This fixed instruction count for iteration has played well into colony’s bid to become a C++ standard library container. C++ containers are not allowed to have iterator operations which do not have O(1) amortized time complexity i.e. the number of instructions it takes to complete the operation must be roughly the same each time. Boolean skipfields require an unknown number of instructions (i.e. number of repetitions of the loop mentioned earlier) to iterate, so they are not appropriate. Time complexity is not terribly important for overall performance nowadays, but it does affect latency, which can sometimes be important.

 

For fields which favour low latency, such as high-performance trading and gaming, an unknown number of instructions can, for example, throw off the timely display of a buffer in a computer game, or miss the window of a particular trading deal. So the swap of skipfield types had a strong benefit there. For me personally though, the most important thing for me was that the number of bits were no longer wasted – they increased performance significantly. In some situations such as low memory scenarios, or where cache space is especially limited, it still might make more sense to go with a bitfield, but that sort of situation usually needs a custom solution anyway.

 

As the years rolled by, colony morphed quite a bit. The high-complexity jump-counting skipfield got replaced with by a low-complexity variant with better overall performance. The initial erased element location storage mechanism, which was a stack of erased element location pointers, got replaced with per-memory-block free lists of individual erased elements, and then by free lists of consecutive blocks of erased elements instead of individual locations. Many functions have been introduced, and much optimization has occurred. Over the past year, it has reached a point of stability.

 

But the core structure has basically remained the same. I got my container with fixed pointer locations for non-erased elements, and the world will – hopefully – get something out of it, as well. I learned a lot about CPUs and architecture in the process. The biggest thing I learned however was that, with the right mindset, you can actually make a difference. That mindset has to have some level of drive to it, but also an element of altruism, really. Because if you’re not doing something in part for yourself, it is difficult to sustain. But if you’re not doing it for others as well, then, long-term there’s no point.

…Oh, and I never did end up making a game 😉