plf::list and the Disassembly of Time Complexity

In his third guest post, Matt Bentley shows us the impact of cache-locality on performance, using plf::list, his implementation of a cache-local linked list as example.

Folks love to make monolithic statements in IT, or in fact in life in general.
It’s one of those things which makes us feel special – here’s that “hidden truth” that everybody else has forgotten, you’re Smart, they’re Dumb and Wrong. So here’s one of those statements: O(1) time complexity operations are better than O(n) time complexity operations. Are they? How long does the O(1) operation take compared to the series of O(n) operations? This seemed an obvious truth in computing for a long time.

As many have pointed out, back “in the day” (‘the day’ means the entire 1980’s in this context) processor speeds were on par with memory speeds, and this meant that for the most part, O(1) was usually better than O(n) for sizeable amounts of data. But as time drew on, what we once considered ‘sizeable’ became smaller and smaller. Operations which might’ve legitimately been O(n) at some point, were now effectively O(1) when it came to what the hardware was doing. Then when we entered the new millennia with long CPU pipelines and a large performance gap between memory and CPUs, data locality became a damn sight more important than time complexity. And so life goes.

The point is not, of course, that data locality is forever going to be more important than time complexity, but it certainly is right now and for most hardware and the majority of situations. In ten years time, if we stumbled across a new form of computing or a way of making memory as fast as CPUs, then those facts might reverse again. There is no reason to suspect that some other aspect of computing might not make a greater performance difference in even two years time. Massively parallel computing is on the rise. Who knows. As Mike Acton has said: “the hardware is the platform, not the software”, ergo, when hardware changes, the approach to software has to change, if stability and performance are relevant – and they always are.

A case in point: linked lists used to be the bees knees. They had O(1) almost-everything! Erase an element in the middle of the container? O(1). Insert an element at the beginning of the container? Still O(1). Find? Okay, so that’s O(n), but the rest are mostly O(1). In the 80’s, dynamic arrays (ie. C++ std::vector style containers) were not only tricky to use (all that pointer invalidation!), but if you inserted or erased anywhere but at back of the container you got a walloping great O(n) operation! No thanks!!! But nowadays the situation is very different and the O(n) aspect less relevant. Even in the context of erasing from random locations, you still tend to get better performance from a std::vector than a std::list, due to the fact that std::vectors have better data locality.

All this is thanks to changes in computing hardware. So a couple of years ago I decided to focus on how linked lists could be made more appropriate for today’s computers. They are, after all, useful for a number of scenarios including multithreaded work (due to low side effects for operations) and large/non-trivially-copyable elements (due to a lack of reallocation during operations). The first thing to do was get rid of individual allocations of list nodes. Data locality matters, as does the number of allocation operations, so this new linked list allocates chunks of multiples nodes. The second thing I did was use ‘free lists’ to keep track of which elements were erased so I could re-use their memory locations later, saving further allocations and increasing data locality.

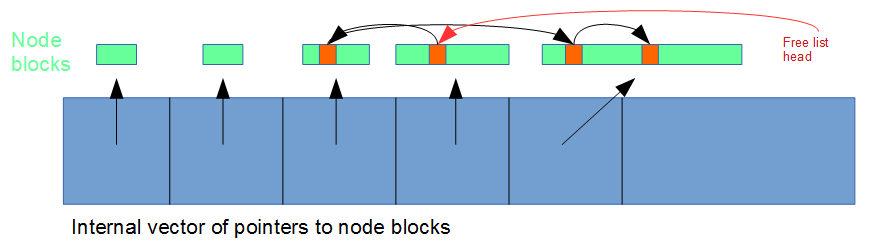
If you’re not familiar with the concept of a free list, in this context there’s a head pointer to the node of the first erased element, and the ‘next’ field of that node points to the next erased node, and so on. I experimented with per-memory-chunk free lists and global free lists, and found per-chunk free lists to be better for a couple of reasons. The first was that they don’t incur a performance penalty when removing a chunk. When using a global free list you have to iterate through the whole free list in order to remove nodes belonging to that chunk. But with a per-chunk free list you erase the free list along with the chunk. The second advantage was that in the context of inserting to the middle of the linked list, they made finding erased nodes close to the insertion point faster. Why is that important? Data locality (again).

If we’re iterating over a regular linked list we’re typically jumping all over the place in memory, unless we’re using a custom allocator, because each node is allocated individually. This slows down performance, due to the fact that CPUs read data from memory in large chunks, and store those in the (much faster) CPU cache. So, if the next element in the linked list doesn’t happen to be in that first memory chunk, it won’t be in the cache either, which means another (slow) read from memory. This means that traditional linked list iteration is typically quite slow. Following pointers doesn’t help much either as it throws off the CPU’s ability to predict the next read location, but there’s nothing much that can be done about that while still having it be a linked list.

So ideally, in a chunk-based linked list, we want to have the elements which are next to each other in the order of iteration also close to each other in memory placement, to minimise the number of memory reads. In the case of insertion, with a per-memory-chunk free list we can quickly (in O(1) time!) check to see if there are any erased elements in the same chunk as the insertion location, and if so, reuse them. Provided we don’t make the chunks too large the likelihood of those two elements (the newly-inserted element and the element it is being inserted next to) being read into cache at the same time increases dramatically.

The final thing I wanted to do was to increase the performance of list sorting. Linked lists have rightly been maligned as being poor choices for sort operations, due to their (again) poor locality and better algorithms being available for containers whose elements are able to be accessed via indexes. Again, back ‘in the day’, linked list sorting was nice because you never had to move any elements around, only write to pointers. Nowadays that’s less relevant, again with the exception of large or non-trivial elements.

So anyway, I hacked the process. I created an array of pointers to the current elements, then sorted it based on the values of the elements those pointers pointed to. Because arrays allow indexing, I was able to use faster sort algorithms which rely on indexing. Then, using those pointers, I processed each node pointed to in turn, making it’s ‘next’ field point to the next element pointed to in the pointer array. Ditto for the ‘previous’ fields, which were pointed to the previous element pointed to in the pointer array. Was this better?

Well. That’s enough sizzle, here’s some steak. On an Intel haswell processor, versus a regular linked list in C++ (std::list), my new abomination (plf::list) had the following stats, on average across multiple type-sizes:

• 333% faster insertion
• 81% faster erasure
• 16% faster iteration
• 72% faster sort
• 492% faster reversal
• 103% faster remove/remove_if
• 62% faster unique
• 826% faster clear (1122550% for trivially-destructible types)
• 1238% faster destruction (6187% for trivially-destructible types)
• 25% faster performance overall in ordered use-case benchmarking (insertion, erasure and iteration only)

(sources: https://plflib.org/benchmarks_haswell_gcc.htm, https://plflib.org/list.htm)

… well heck, I guess that worked huh.
This was further validated once I released it to the public, as I received reports from users whose overall program performance increased by 16% or more when switching from std::list to plf::list. Now you still shouldn’t use linked lists in situations which they’re not appropriate for, and there’s plenty of areas where that’s the case – but if you do have to use one, you’re going to be better off using one that’s designed for today’s computer platforms, not for platforms 40 years ago.

One thing remains to be explained, and that’s the phenomenal increase in speed for destruction and clear’ing, particularly for trivially-destructible types. You might be able to guess this one: in a normal linked list, destruction involves iterating through the list via the previous and next pointers, destructing each element and deallocating the node. For starters, that’s a lot of deallocations. But secondly, you’re forced to iterate over the list regardless of whether you need to destruct the elements. For a chunk-based linked list, you don’t have to iterate in this scenario – you just deallocate the chunks.

But even when you do have to destruct the elements it’s still faster. This is because when you’re destructing/clear’ing a container, the order in which you destruct elements doesn’t matter. Which means in the context of plf::list we can iterate over the element chunks linearly in memory, rather than following the actual linked list’s sequence. Which in turn increases data locality and prefetching performance, thereby reducing iteration time. This process of linearly iterating over elements in memory is also used by the reversal, sort and remove/remove_if operations.

So what can we learn from all this? Obviously, data locality matters a lot at the moment, but more importantly, things change. While it is possible that my linked list will always remain faster than a traditional linked list due to the reduced number of allocations necessary, its also possible that within the next decade or two it’s performance advantages will reduce significantly as CPU’s change and, hopefully, memory speeds increase. But we don’t know.
As always, hardware is the key. All hail hardware.